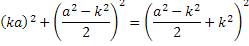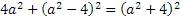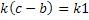Постановка задачи
В 1900г. на 1 Международном математическом конгрессе, известный математик Давид Гильберт[1] поставил перед математиками всего мира 23 задачи. Эти задачи принято называть "Проблемами Гильберта".
Решением десятой проблемы Гильберта стало признание ее неразрешимости, доказанное советским математиком Ю.В.Матясевичем [2] в 1970г.
Доказательство неразрешимости Матиясевича признано как единственно допустимое, но возможно это не так.
Итак, для того, чтобы опровергнуть, либо подтвердить это доказательство нужно вначале напомнить задачу, определенную Д.Гильбертом в 10-й проблеме.
«Пусть задано диофантово уравнение с произвольными неизвестными и целыми рациональными числовыми коэффициентами. Указать способ, при помощи которого возможно после конечного числа операций установить, разрешимо ли это уравнение в целых рациональных числах»
То есть нужно найти некий алгоритм, при помощи которого возможно находить натуральные (целочисленные) значения для произвольных неизвестных.
Решение проблемы
Самое известное уравнение Диофанта[3] это формула Пифагора[4].

Известны также так называемые «тройки Пифагора», целочисленные значения для неизвестных «a,b,c»
3,4,5; 5,12,13; 7,24,25 и т.д. Эти тройки имеют два сходства: первое – квадрат первого числа равен сумме двух других чисел, второе – разница между вторым и третьим числом равна 1. Следовательно, можно предположить, что это не случайные совпадения. Исходя из этого, составим равенства

Теперь, используя все эти формулы, составим уравнения
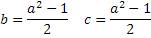
Подставим эти уравнения в формулу Пифагора


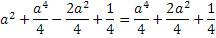

Получилось равенство значений правой и левой сторон уравнения. Это можно считать доказательством существования алгоритма нахождения натуральных значений «пифагоровых троек». Итак, обобщим формулы алгоритма и собственно получившийся алгоритм
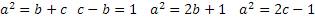

Но эти формулы диофантовы лишь для нечетных чисел, хотя при постановке в формулы четных чисел для «а» также можно найти значения двух других чисел «b» «c», эти значения будут рациональными, но не целыми числами.
Пример № 1
«а»= 8



Также, применяя этот алгоритм, можно находить соответствующие значения «троек» для любых рациональных чисел.
Пример № 2
a=2,5

Так как закономерностью алгоритма является соотношение

то значение «c» можно найти, добавив к числу «b» 1
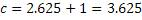


Алгоритм верен и для дробей
Пример № 3



И для квадратных корней
Пример № 4

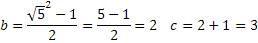

Применяя этот алгоритм, можно находить значения практически всех троек Пифагора.
Однако существуют тройки, которые не подходят к этому алгоритму: 20,21,29; 12,35,37; 14,48,50; 15,36,39 и т.д.
Следовательно: этот алгоритм нельзя назвать единым способом нахождения всех Пифагоровых троек. Но не будем опускать руки. Разберем пример с числовой тройкой 20,21,29
Выше я привел пример с а=2.5, значения b и с были соответственно 2.625 и 3.625, если предположить, что число 20 это производная числа 2.5, то получится коэффициент равный 8, и следовательно числа 20,21,29 не являются взаимно простыми. Проверим это предположение

Коэффициент кратности исходного уравнения совпадает с разностью между «b» и «с». Чтобы выяснить совпадение это или закономерность, проверим другую тройку 15,36,39. Разница между «b» и «с» составляет 3
Пример № 5

Получилась уже известная тройка 5,12,13, то есть удовлетворяющая условиям исходного или первичного алгоритма, что и требовалось подтвердить.
Остается еще один вопрос. При возведении числа в квадрат не важно, с каким знаком: плюсом или минусом, результат все равно будет иметь положительное значение. Это важно для подтверждения правильности алгоритма. В примере 3, число «b» имеет отрицательное значение, но если поменять знак ничего не изменится, и результат останется прежним. Если поменять знак числа b с минуса на плюс, разница между b и с, уменьшится в 9 раз
Пример № 6

Исходя из вышеизложенного, можно предположить, что разница является коэффициентом кратности исходного уравнения. Для проверки этого предположения нужно разделить числа тройки на получившийся коэффициент.
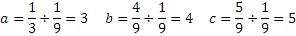
И вновь получилась уже известная тройка 3,4,5.
На основании полученных результатов, можно записать алгоритм кратности

Осталось объединить получившиеся алгоритмы в один универсальный.

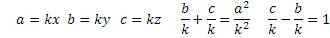
Теперь можно вычислять абсолютно все пифагоровы тройки, зная или задавая значение любого одного числа из тройки и задавая кратность уравнению.
Задача № 1
Найти значения чисел «а» и «b» в уравнении

Условия задачи
Дано:
Значение числа «с»=161
Коэффициент кратности уравнения «k»=7
Воспользуемся формулами универсального алгоритма

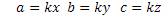


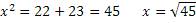

Проверим получившийся результат
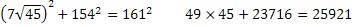
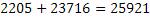
Задача решена, числа найдены.
Задача № 2
Требуется найти натуральные значения чисел «b» и «с» для уравнения

Условия задачи
Дано:


Воспользуемся формулами, для нахождения исходных «троек»



Подставим числа в формулу

Теперь нужно привести все числа к общему знаменателю
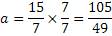
Остается воспользоваться формулой кратности


и разделить числа на коэффициент кратности,



Проверяем

Задача решена, числа найдены.
Из этой задачи видно, что знаменатель нужно помножить на числитель. Поэтому можно создать следующий алгоритм для произвольных «k» и «а».
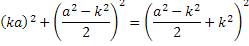
Проверим действие этого алгоритма
Пример № 7





Алгоритм работает. Для генерации пифагоровых троек можно использовать как универсальный алгоритм, так упрошенный.
Для чисел кратным 4-ем существует еще один алгоритм. Его можно использовать для упрощенного нахождения пифагоровых троек.
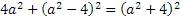 Пример № 8
Пример № 8


Получилась уже известная тройка.
Доказательство теоремы Ферма
Постановка вопроса о разрешимости диофантовых уравнений подразумевала также доказательство теоремы Ферма[5]. Почему же не может существовать целочисленные значения для уравнений вида

При

Собственно от формулы Пифагора это уравнение отличается только значением степени, поэтому формула Пифагора принадлежит к этим уравнениям.
А раз она принадлежит к данным уравнениям, то для нахождения решений можно применить универсальный алгоритм. Для этого нужно это произвольное уравнение перевести в степень 2

Упростим уравнение

Теперь можно применить одну из формул алгоритма
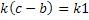
Для нахождения значений этого уравнения, кратностью можно пренебречь, так как в любом случае существует исходная тройка взаимно простых чисел. Поэтому применим формулу исходного алгоритма


По условиям алгоритма, должно получиться равенство

Предположим, что такое равенство возможно. Но коэффициент числа «b» меньше 1, так как сумма, которую представляет число «с», больше слагаемого, которое представляет число «b».

Из этого следует что

что соответствует утверждению Ферма о невозможности существования натуральных чисел, и не соответствует условиям алгоритма, это наглядно показывает ,что не существует целочисленных решений для уравнений вида

При

А так как в приведенных выше примерах доказано, что алгоритм является верным не только для натуральных, но и для всех рациональных чисел, то можно уверенно утверждать: не существует даже рациональных решений для уравнений этого вида.
Итак, подведем итог этого исследования.
1) Доказано, что существует универсальный алгоритм или, как указано в 10-й проблеме Гильберта, единый способ, при помощи которого возможно после конечного числа операций установить разрешимо или нет уравнение вида

в целых рациональных числах
2) Доказано, что при помощи универсального алгоритма решение в натуральных и рациональных числах возможно для этого уравнения при n=2
3) Доказано, что для уравнений

При

Решений в натуральных и рациональных числах не существует.
Сноски
[1] Ю. В. Матиясевич, Десятая проблема Гильберта – М., Наука, 1993
[2] Давид Гильберт (23.01.1862 – 14.02.1943) математик-универсал, внес значительный вклад в развитие многих областей математики.
[3] Диофант Александрийский древнегреческий математик, живший в 3-ем веке н.э.
[4] Пифагор Самосский ( 570-490г до н.э.) древнегреческий философ, математик.
[5] Пьер де Ферма (17.09.1601 – 12.01. 1665) французский математик-самоучка.
Оглавление
Постановка задачи
Решение проблемы
Доказательство теоремы Ферма



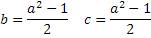


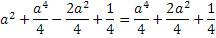

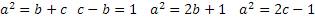






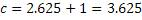






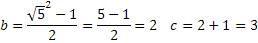




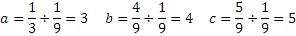


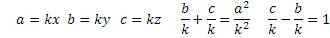


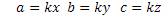


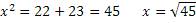

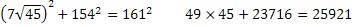
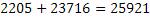


 Воспользуемся формулами, для нахождения исходных «троек»
Воспользуемся формулами, для нахождения исходных «троек»




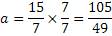

 и разделить числа на коэффициент кратности,
и разделить числа на коэффициент кратности,